QuickSort

In this tutorial, we will learn the quicksort algorithm and its implementation in C.

QuickSort is a sorting algorithm that works based on the divide-and-conquer strategy. It works as follows:

1. Choose an element as pivot from the array.
2. Position the pivot element in such a way that all elements less than the pivot appear before it and all elements greater than the pivot appear after it (equal values can go either way).
3. Sort the two sub-arrays recursively.

The pivot element can be selected in any of the following ways:

• Pick first element as pivot (Explained Here).
• Pick last element as pivot.
• Pick a random element as pivot.
• Pick median as pivot.

Working of QuickSort Algorithm

Suppose we have to sort the following array of 6 elements using the quicksort algorithm.

1. Choose the pivot element

Here we choose the first element as the pivot.

2. Rearrange the elements

Now we have to rearrange the array elements in such a way that all elements less than the pivot appears before it and all elements greater than the pivot appears after it as shown in the figure.

The following steps are done for rearranging the array:

Create three pointers, pivot = 0, left = 0 and right = n-1.

Then, the comparison is done as follows:

1. Starting from right compare each element with pivot.
   1. If pivot < right then, continue comparing until right = pivot.
   2. If pivot > right then, swap two values and goto step 2.
   3. Set pivot = right.
2. Starting from left compare each element with pivot
   1. If pivot > left then, continue comparing until left = pivot.
   1. If pivot < left then, swap two values and goto step 1.
   2. Set pivot = left.

Set the pointers and start comparing from the right.

Since pivot < right is true, continue comparing with the next element.

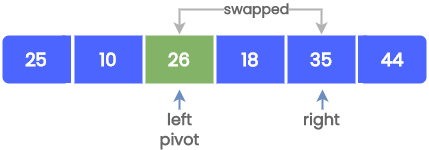
Now pivot > right, so swap them and set pivot = right.

Start comparing from left to right. Since pivot > left, continue comparing.

Since pivot < left, swap them and set pivot = left.

Continue the process until we get the following array where the pivot is placed in the correct position.

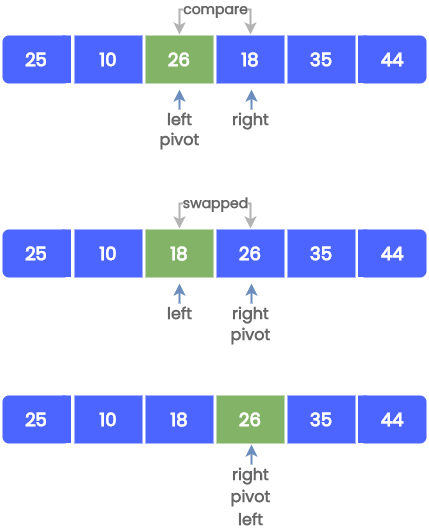
3. Dividing Array

Pivot elements are chosen separately for the left and right sub-arrays and step 2 is then repeated. We get the following array after the quicksort algorithm has been completed.

The formal algorithm for quicksort is given below:

Algorithm: PARTITION (ARR, BEG, END, LOC)

1: SET LEFT = BEG, RIGHT = END, PIVOT = BEG, FLAG = 0
2: Repeat Steps 3 to 6 while FLAG = 0
3: Repeat while ARR[PIVOT] <= ARR[RIGHT] AND PIVOT != RIGHT
‎      SET RIGHT = RIGHT-1
‎   [END OF LOOP]
4: IF PIVOT = RIGHT
‎      SET FLAG=1
‎   ELSE IF ARR[PIVOT] > ARR[RIGHT]
‎      SWAP ARR[PIVOT] with ARR[RIGHT]
‎      SET PIVOT = RIGHT
‎   [END OF IF]
5: IF FLAG = 0
‎      Repeat while ARR[PIVOT] >= ARR[LEFT] AND PIVOT != LEFT
‎         SET LEFT = LEFT+1
‎      [END OF LOOP] 
6: IF PIVOT = LEFT
‎      SET FLAG = 1
‎   ELSE IF ARR[PIVOT] < ARR[LEFT]
‎      SWAP ARR[PIVOT] with ARR[LEFT]
‎      SET PIVOT = LEFT
‎   [END OF IF]
‎[END OF IF]
‎7: [END OF LOOP]
‎8: END

Algorithm: QUICK_SORT (ARR, BEG, END)

1: IF (BEG < END)
      CALL PARTITION (ARR, BEG, END, LOC)
      CALL QUICKSORT(ARR, BEG, LOC-1)
      CALL QUICKSORT(ARR, LOC+1, END)
[END OF IF]
2: END

Quicksort code in C

#include <stdio.h>
#include <conio.h>

int partition(int a[], int beg, int end);
void quick_sort(int a[], int beg, int end);

int main()
{
    int arr[6]={26, 10, 35, 18, 25, 44}, i, n=6;
    
    quick_sort(arr, 0, n - 1);

    printf("\n The sorted array is: \n");
    for (i = 0; i < n; i++)
        printf(" %d\t", arr[i]);

    return 0;
}
int partition(int a[], int beg, int end)
{
    int left, right, temp, pivot, flag;
    pivot = left = beg;
    right = end;
    flag = 0;

    while (flag != 1)
    {
        while ((a[pivot] <= a[right]) && (pivot != right))
            right--;
        if (pivot == right)
            flag = 1;
        else if (a[pivot] > a[right])
        {
            temp = a[pivot];
            a[pivot] = a[right];
            a[right] = temp;
            pivot = right;
        }
        if (flag != 1)
        {
            while ((a[pivot] >= a[left]) && (pivot != left))
                left++;
            if (pivot == left)
                flag = 1;
            else if (a[pivot] < a[left])
            {
                temp = a[pivot];
                a[pivot] = a[left];
                a[left] = temp;
                pivot = left;
            }
        }
    }
    return pivot;
}
void quick_sort(int a[], int beg, int end)
{
    int pivot;
    if (beg < end)
    {
        pivot = partition(a, beg, end);
        quick_sort(a, beg, pivot - 1);
        quick_sort(a, pivot + 1, end);
    }
}

The Complexity of QuickSort Algorithm

• Best case – O(n log n)
• Worst-case – O(n²)
• Average case – O(n log n)

Pros and Cons of QuickSort

Quicksort is faster than other algorithms such as bubble sort, selection sort, and insertion sort. It can be used to sort arrays of various sizes. On the other hand, quicksort is complicated and massively recursive.