Queue

A Queue is a linear data structure in which deletions can only occur at one end, known as the front, and insertions can only occur at the other end, known as the rear. It is similar to the real-life queue where the first person entering the queue is the first person who comes out of the queue. Thus queues are also called FIFO(First In First Out) lists.

Basic Operations of Queue

A queue allows the following basic operations:

• Enqueue – Add new element to the end of the queue.
• Dequeue – Remove an element from the front of the queue.

Every queue includes two pointers, FRONT and REAR, which indicate the position where deletion and insertion can be performed. Initially, values of FRONT and REAR is set to -1.

Enqueue Operation

Inserting a new element in the position pointed by REAR is called the enqueue operation. We must check if the queue is full before insertion. After the enqueue operation the REAR is incremented by 1 and will point to the newly inserted element.

For inserting the first element in a queue, the value of FRONT has to be set to 0.

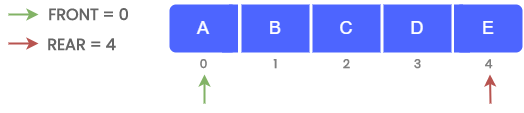
Consider a queue of size 5. Suppose we have to insert A, B, C, D and E into the queue. The following changes will be made to the queue.

Dequeue Operation

Deleting an element in the position pointed by FRONT is called the dequeue operation. We must check if the queue is empty before deletion. After the dequeue operation, the FRONT is incremented by 1.

After deleting the last element in a queue, the value of FRONT and REAR has to be set to 0.

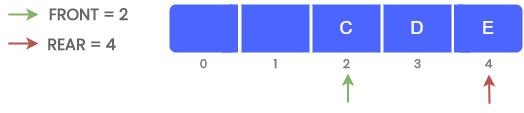
Consider the following example where we dequeue elements one by one until the queue becomes empty.

Representation of Queues

Queue is usually represented in the computer using a linear array or a one-way linked list.

Array Representation of Queue

A queue can be represented in a program by using a linear array of elements and three pointer variables FRONT, REAR and MAX.

The queue is empty if FRONT = REAR = -1. The queue is full if FRONT =1 and REAR = MAX - 1.

The size of the above queue is 5. It has 3 elements A, B and C. The FRONT, REAR and MAX pointers will have values 0, 2 and 5 respectively.

The algorithms for enqueue and dequeue operations are given below.

Algorithm: ENQUEUE(QUEUE, MAX, FRONT, REAR, ITEM)

Step 1: IF REAR = MAX-1
            Write OVERFLOW
            Goto step 4
        [END OF IF]
Step 2: IF FRONT=-1 and REAR=-1
            SET FRONT = REAR = 0
            ELSE
            SET REAR = REAR + 1
        [END OF IF]
Step 3: SET QUEUE[REAR] = ITEM
Step 4: EXIT

• Print overflow and exit if the queue is full.
• For adding first element make FRONT = 0.
• Increment REAR by 1.
• Insert new element in the position pointed by REAR.

Algorithm DEQUEUE(QUEUE, MAX, FRONT, REAR, ITEM)

Step 1: IF FRONT = -1 OR FRONT > REAR
            Write UNDERFLOW
        ELSE
            SET ITEM = QUEUE[FRONT]
            SET FRONT = FRONT + 1
        [END OF IF]
Step 2: EXIT

• Print underflow and exit if the queue is empty.
• Return the value pointed by FRONT.
• Increment FRONT by 1.
• Set FRONT = REAR = -1 for the last element.

Linked Representation of Queues

The disadvantage of using an array to represent a queue is that the array must be specified to have a fixed size. If the array size cannot be known ahead of time, then the linked representation is used.

The HEAD pointer of the linked list is used as the FRONT. Also, use another pointer called REAR to store the address of the last element of the queue.

The algorithms for enqueue and dequeue operations are given below.

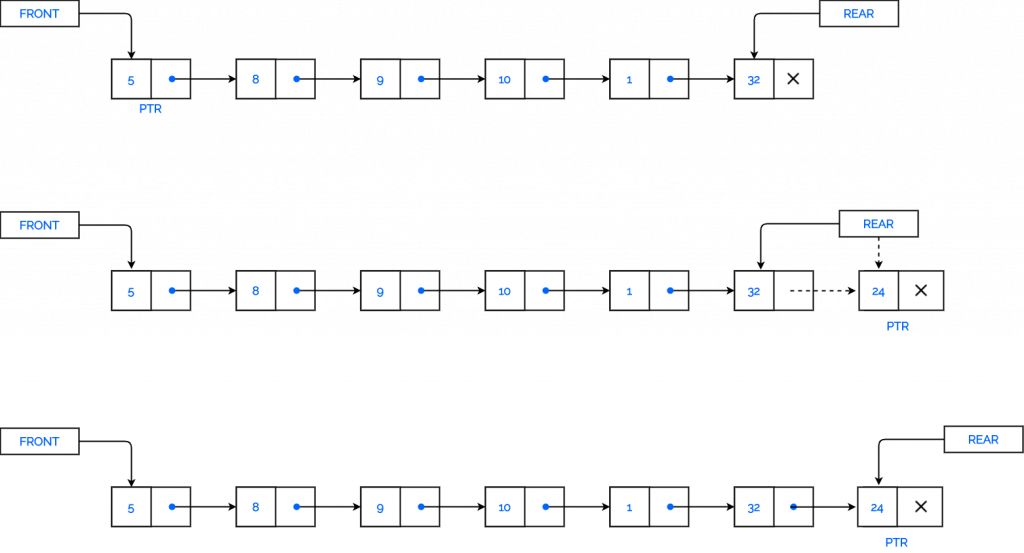
Algorithm: LINK_ENQUEUE

Step 1: Allocate memory for the new node and name it as PTR
Step 2: SET PTR -> DATA = VAL
Step 3: IF FRONT = NULL
            SET FRONT = REAR = PTR
            SET FRONT -> NEXT = REAR -> NEXT = NULL
        ELSE
            SET REAR -> NEXT = PTR
            SET REAR = PTR
            SET REAR -> NEXT = NULL
        [END OF IF]
Step 4: END

Algorithm: LINK_DEQUEUE

Step 1: IF FRONT = NULL
            Write Underflow
            Go to Step 5
        [END OF IF]
Step 2: SET PTR = FRONT
Step 3: SET FRONT = FRONT -> NEXT
Step 4: FREE PTR
Step 5: END

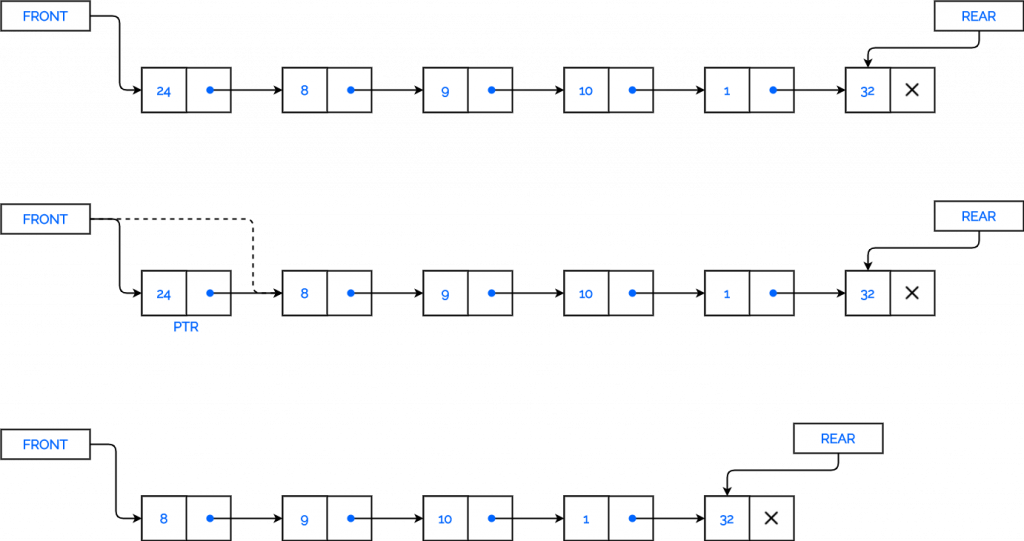
Disadvantage of Queue

Look at the following queue.

You cannot insert a new value now, because the queue is completely full. Consider the following case: two consecutive deletions are made.

Even though there is enough space to hold a new element, the overflow condition still occurs since the condition REAR = MAX – 1 is still valid. This is a major drawback of a linear queue. A solution to this problem is to make the queue circular.

Types of Queues

A queue data structure can be classified into the following types:

• Circular Queue.
• Priority Queue.
• Dequeue.

Application of Queue

• Manage resource sharing such as CPU scheduling, disk scheduling..etc
• When data is sent and received between two processes asynchronously.
• Hadling of inrepputs in real time.
• Call waiting systems in call centers.