An expression tree is a special type of binary tree that is used to store algebraic expressions. In an expression tree, each internal node corresponds to the operator and each leaf node corresponds to the operand.
Consider the algebraic expression given as: X = (a + b) - (c * d). This can be represented using a binary tree as follows:

The in-order traversal of the tree returns the infix expression. Similarly, the pre-order and post-order traversal of the expression tree will return prefix and postfix expression respectively.
Constructing an expression tree
An expression tree can be constructed with the help of a stack. Repeat the following steps for every character in the postfix expression:
- If the character is an operand, PUSH it on to the stack.
- If the character is an operator, POP two values from the stack and insert them as the child of operator. A pointer to the new root is pushed on to the stack.
Consider the postfix expression a b - c * . The following steps are done to create an expression tree.
Since the first two characters are operands, PUSH it onto the stack.

When the - symbol is read, a and be are popped from the stack and is added as the child of node - . A pointer to the new node is now pushed onto the stack.

Now c is read and is pushed onto the stack.

Finally, the operator * is read, so we pop c and - from the stack and add it as the child of node * .
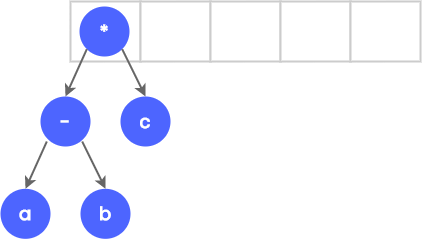
When the operation is completed, the pointer to the root of three remains on the stack.
