Binary Tree Traversal Algorithm Without Recursion

In this tutorial, you will learn the implementation of different tree traversal algorithms, which were specified recursively in the last tutorial, by means of non-recursive procedures using stacks.

Pre-order Traversal Without Recursion

The following operations are performed to traverse a binary tree in pre-order using a stack:

1. Start with root node and push onto stack.
2. Repeat while the stack is not empty
   1. POP the top element (PTR) from the stack and process the node.
   2. PUSH the right child of PTR onto to stack.
   3. PUSH the left child of PTR onto to stack.

Consider the following tree.

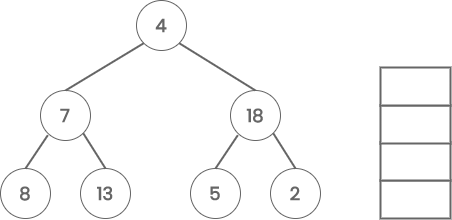
Start with node 4 and push it onto the stack.

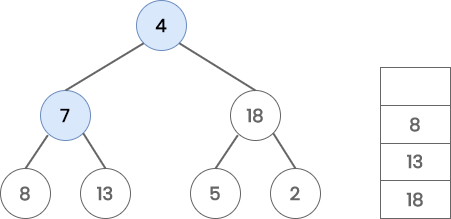
Since the stack is not empty, POP 4 from the stack, process it and PUSH its left(7) and right(18) child onto the stack.

Repeat the same process since the stack is not empty. POP 7 from the stack, process it and PUSH its left(8) and right (13) child onto the stack.

Again, POP 8 from the stack and process it. Since it has no right or left child we don’t have to PUSH anything to the stack.

Now POP 13 from the stack and process it. We don’t have to PUSH anything to the stack because it also doesn’t have any subtrees.

POP 18 from the stack, process it and PUSH its left(5) and right(2) child to the stack.

Similarly POP 5 and 2 from the stack one after another. Since both these nodes don’t have any child, we don’t have to PUSH anything onto the stack.

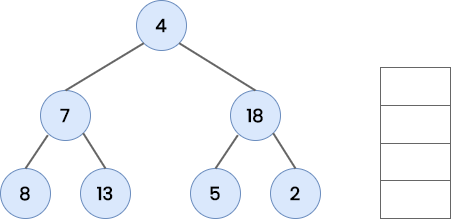
The nodes are processed in the order [ 4, 7, 8, 3, 18, 5, 2 ]. This is the required preorder traversal of the given tree.

The formal algorithm is given below:

1. Set TOP = 1. STACK[1] = NULL and PTR = ROOT.
2. Repeat Steps 3 to 5 while PTR ≠ NULL:
3.    Apply PROCESS to PTR->DATA.
4.    If PTR->RIGHT ≠ NULL, then:
‎        Set TOP = TOP + 1, and STACK[TOP] = PTR->RIGHT.
‎      [End of If]
5.    If PTR->LEFT ≠ NULL, then:
‎         Set PTR = PTR -> LEFT.
‎      Else:
‎         Set PTR = STACK[TOP] and TOP = TOP - 1.
‎      [End of If]
‎   [End of Step 2 loop.]
6. Exit.

In-order Traversal Without Recursion

The following operations are performed to traverse a binary tree in in-order using a stack:

1. Start from the root, call it PTR.
2. Push PTR onto stack if PTR is not NULL.
3. Move to left of PTR and repeat step 2.
4. If PTR is NULL and stack is not empty, then Pop element from stack and set as PTR.
5. Process PTR and move to right of PTR , go to step 2.

Consider the following tree.

Start with node 4 and call it PTR. Since PTR is not NULL, PUSH it onto the stack.

Move to the left of node 4. Now PTR is node 7, which is not NULL. So PUSH it onto the stack.

Again, move to the left of node 7. Now PTR is node 8, which is not NULL. So PUSH it onto the stack.

When we move again to the left of node 8, PTR becomes NULL. So POP 8 from the stack. Process PTR (8).

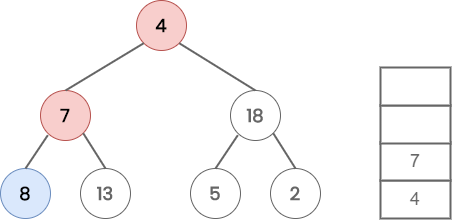
Move to the right child of PTR(8), which is NULL. So POP 7 from the stack and process it. Now PTR points to 7.

Move to the right child(13) of PTR and PUSH it onto the stack.

Move to the left of node 13, which is NULL. So POP 13 from the stack and process it.

Since node 13 don’t have any right child, POP 4 from the stack and process it. Now PTR points to node 4.

Move to the right of node 4 and put it on to the stack. Now PTR points to node 18.

Move to the left(5) child of 18 and put it onto the stack. Now PTR points to node 5.

Move to the left of node 5, which is NULL. So POP 5 from the stack and process it.

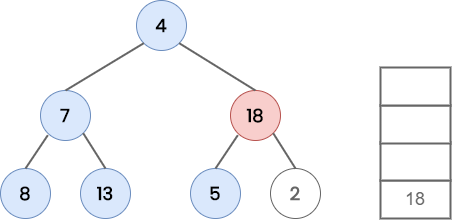
Now, move to the right of node 5, which is NULL. So POP 18 from the stack and process it.

Move to the right(2) of node 18 and PUSH it on to the stack.

Since node 2 has left child, POP 2 from the stack and process it. Now the stack is empty and node 2 has no right child. So stop traversing.

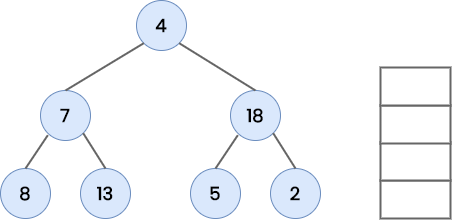
The nodes are processed in the order [ 8, 7, 13, 4, 5, 18, 2 ] . This is the required in order traversal of the given tree.

The formal algorithm is given below:

1. Set TOP = 1, STACK[1] = NULL and PTR = ROOT.
2. Repeat while PTR ≠ NULL:
‎      (a) Set TOP = TOP + 1 and STACK[TOP] = PTR.
‎      (b) Set PTR = PTR->LEFT.
‎   [End of loop.]
3. Set PTR = STACK[TOP] and TOP = TOP - 1.
4. Repeat Steps 5 to 7 while PTR ≠ NULL:
5.    Apply PROCESS to PTR->INFO.
6.    If PTR->RIGHT ≠ NULL, then:
‎         (a) Set PTR = PTR->RIGHT.
‎         (b) Go to Step 3.
‎      [End of If]
7. Set PTR = STACK[TOP] and TOP = TOP -1.
‎   [End of Step 4 loop.]
8. Exit.

Post-order Traversal Without Recursion

The post order traversal algorithm is more difficult to implement than the previous two algorithms. The following operations are performed to traverse a binary tree in post-order using a stack:

1. Start from the root, call it PTR.
2. Push PTR onto stack if PTR is not NULL.
3. Move to left of PTR and repeat step 2.
4. If PTR has a right child R, then PUSH -R onto the stack.
5. Pop and process positive element from stack and set as PTR.
6. If a negative node is popped, (PTR = -N), then set PTR = N and go to step 2.

The formal algorithm is given below:

1. Set TOP = 1. STACK[1] = NULL and PTR = ROOT.
2. Repeat Steps 3 to 5 while PTR ≠ NULL:
3.    Set TOP = TOP + 1 and STACK[TOP] = PTR.
4.    If PTR->RIGHT ≠ NULL. then: [Push on STACK. ]
‎         Set TOP = TOP + 1 and STACK[TOP] = PTR->-RIGHT.
‎      [End of If structure.]
5.    Set PTR = PTR->LEFT. [Updates pointer PTR.]
‎   [End of Step 2 loop.]
6. Set PTR = STACK[TOP] and TOP = TOP - 1.
7. Repeat while PTR > 0:
‎      (a) Apply PROCESS to PTR->INFO.
‎      (b) Set PTR = STACK[TOP] and TOP = TOP - 1.
‎   [End of loop.]
8. If PTR < 0, then:
‎      (a) Set PTR = -PTR.
‎      (b) Go to Step 2.
‎   [End of If structure]
9. Exit.