Binary Tree

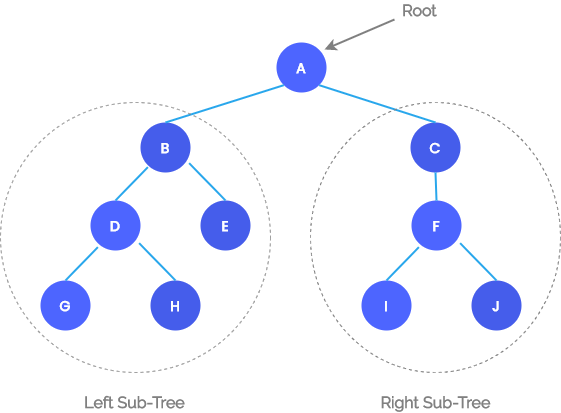
A Binary tree is a special tree where each node can have no more than two children. A non-empty binary tree consist of the following:

• A node called the root node.
• A left sub-tree.
• A right sub-tree.

Both the sub-trees are themselves binary trees.

Types of Binary Trees

Complete Binary Tree

The tree T is said to be complete if,

• All it’s levels, except possibly the last, must be completely filled.
• All the leaf nodes must appear as far left as possible.

Full Binary Tree

A full binary tree is a special type of tree in which the leaf nodes will have zero children and other non-leaf nodes will have exactly 2 children.

Representation of Binary Tree

Binary trees can be maintained in memory using either an array or a linked list.

Sequential representation of binary trees

The simplest technique for representing a binary tree is to store the elements using a one-dimensional array.

Suppose we are using a one-dimensional array TREE to store the elements of a tree. The rules for a sequential binary tree are as follows:

• The root of the tree will be stored in TREE[0].
• If an element is stored in TREE[K], then
  • It’s left child is stored in TREE[2K + 1].
  • It’s right child is stored in TREE[2K + 2].

A tree of height h will require an array of maximum size 2^h-1. A tree is empty if TREE[0] = NULL.

The following figure shows a binary tree and its corresponding sequential representation.

This method is inefficient unless the tree is (almost) full. Also, it is not possible to add a new node if the tree is already full.

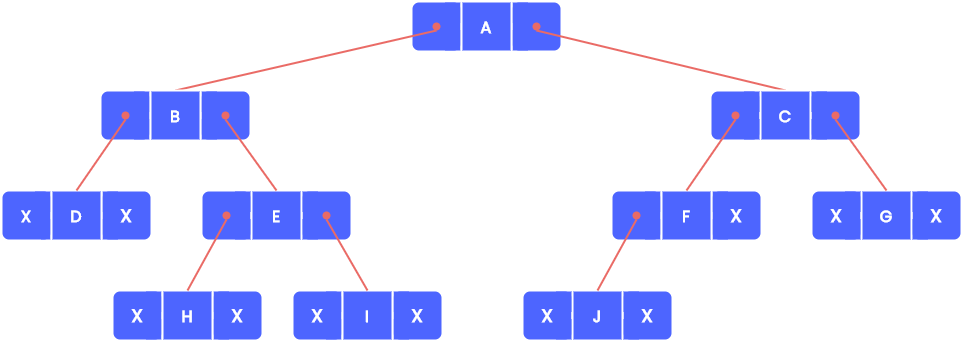
Linked representation of binary trees

Every node in a linked representation of binary tree will contain three parts:

• The data element.
• A pointer to the left node.
• A pointer to the right node.

It can be represented by a structure.

struct node {
    struct node *left;
    int data;
    struct node *right;
};

The root node is pointed by a pointer ROOT. The tree is empty if ROOT = NULL

The schematic diagram of the linked representation of the binary tree is shown below.

Applications of Binary Tree

• For rapid and easy access to data.
• Routing algorithms.
• To implement heap data structure.
• Syntax tree, Binary Search Tree, Hash Trees, Treap, T-tree, etc.